Laser-Ion Acceleration

1. Basic laser concept: resonator, active medium, pump

To understand high-power ultrashort-pulse lasers, we start from the basic ingredients of any laser:

• Active medium — provides optical gain via stimulated emission.
• Pump — supplies energy to create a population inversion.
• Optical resonator — cavity that selects and amplifies resonant modes.

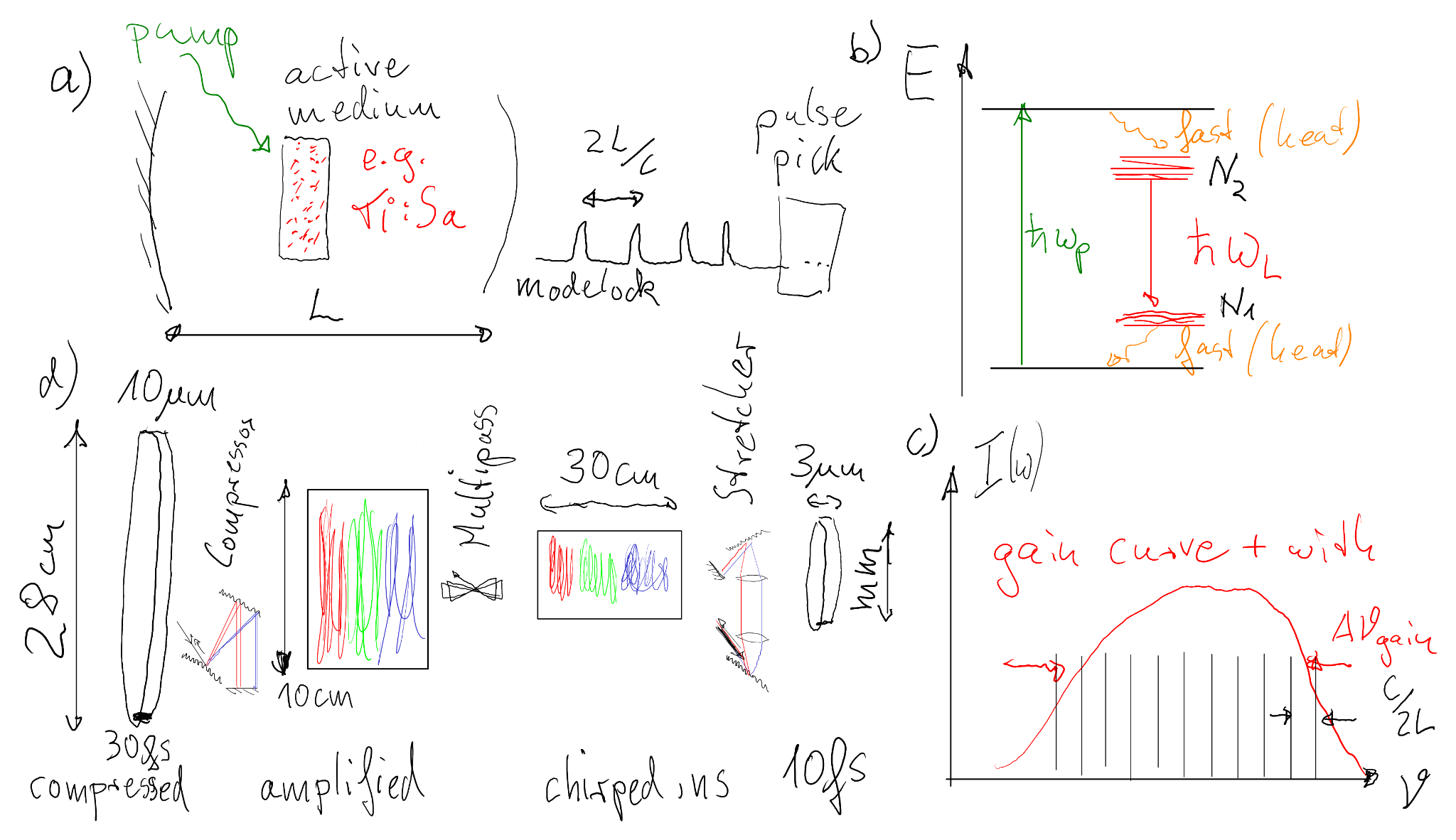
The pump (flashlamp, diode laser, or another laser) excites electrons in the active medium from lower-lying states to higher-lying energy levels. Stimulated emission then amplifies light at the transition between an upper and a lower laser level. The resonator mirrors reflect the light back and forth, so the light passes many times through the medium and experiences exponential gain until losses and gain balance in steady state. Panel (a) of Figure 3.1 shows this schematically: a gain medium inside a resonator with an external pump.

2. Energy levels and population inversion

Laser action requires population inversion: more atoms in the upper laser level than in the lower. This cannot be achieved in a simple two-level system — see panel (b) of Fig. 3.1.

2.1 Why a two-level system cannot be inverted

In a two-level system, pump and laser transition connect the same states. Strong pumping can at best equalize the populations, not invert them.

2.2 Three-level and four-level systems

A three-level system adds a higher pump level; inversion is possible but requires pumping more than half of all atoms out of the ground state — inefficient.

A four-level system adds a level below the lower laser level that empties rapidly. The lower laser level is then essentially unoccupied, so even a small upper-level population yields inversion. Ti:sapphire operates in an effective four-level (or quasi-four-level) scheme.

3. Gain bandwidth and longitudinal modes

The active medium sets both the central wavelength and the gain bandwidth. For ultrashort pulses, Ti:sapphire is central: broad gain near 800 nm (panel (c) of Fig. 3.1).

A linear resonator of length \(L\) supports longitudinal frequencies

\[ \nu_n = n \frac{c}{2L}, \qquad n = 1,2,3,\dots, \qquad \Delta\nu = \frac{c}{2L}. \]

Typically many such modes lie within the gain bandwidth.

3.1 From many modes to short pulses: mode locking

A single longitudinal mode gives essentially continuous-wave (CW) output. If many modes oscillate with fixed phase relationships (mode locking), constructive interference produces a train of short pulses — a direct consequence of the Fourier theorem.

A Ti:sapphire oscillator typically delivers 20–100 fs pulses at \(\sim 80\) MHz repetition rate (panel (a) of Fig. 3.1).

4. From oscillator pulse to high energy: nonlinearities and damage

A single mode-locked oscillator pulse typically has:

• energy \(\sim 1\) nJ,
• duration \(\sim 20\)–30 fs,
• beam diameter \(\sim 1\) mm.

That is far too little for laser–plasma acceleration. We need amplification to the joule level — but sending such a short, intense pulse directly through an amplifier chain causes:

• nonlinear optical effects that distort pulse and beam,
• optical damage that destroys components.

4.1 Nonlinear polarization

The polarization response can be expanded as \[ P(\mathbf r,t) = \chi^{(1)} E + \chi^{(2)} EE + \chi^{(3)} EEE + \cdots \] At low intensity the linear term dominates. At high field strength the third-order term \(\chi^{(3)} E^3\) becomes important in symmetric media (glasses, gases), giving:

• self-phase modulation (SPM) — intensity-dependent phase, spectral broadening,
• self-focusing (Kerr effect) — intensity-dependent refractive index, beam collapse.

These effects are useful inside the oscillator (passive mode locking via self-focusing) but detrimental in high-power amplifiers.

4.2 Time scales of damage

• Nanosecond pulses: mainly thermal damage (melting, cracking).
• Femtosecond pulses: “cold” ablation — ionization faster than heat diffusion.

In the amplification chain we want to avoid nonlinearities and damage; extreme intensities are reserved for the final focus and interaction region (Lecture 2, §8).

5. Chirped pulse amplification (CPA)

Panel (d) of Fig. 3.1 summarizes chirped pulse amplification. The central idea: keep intensity low during amplification. For a pulse, \[ I \approx \frac{E_{\text{pulse}}}{A\,\tau}, \] so we increase beam area \(A\) and pulse duration \(\tau\) while raising \(E_{\text{pulse}}\).

5.1 Stretching

A single femtosecond pulse from the oscillator passes through a grating stretcher (or similar dispersive system). Frequency components follow different path lengths; the pulse acquires a linear chirp and stretches from tens of femtoseconds to hundreds of picoseconds or ~1 ns. Peak intensity drops by many orders of magnitude.

5.2 Amplification

The stretched pulse is amplified in several Ti:sapphire stages, pumped by energetic green lasers (e.g. frequency-doubled Nd:YAG). At each stage the beam diameter is increased to keep fluence and intensity below nonlinear limits (B-integral \(\lesssim 1\)). The largest crystals allow pulse energies up to tens of joules.

5.3 Compression

After amplification, the chirped pulse is expanded once more, propagated in vacuum, and sent through a grating compressor — essentially the time-reversed stretcher. The chirp is removed and the pulse recompresses toward its transform limit. Transport to the experiment remains in vacuum to avoid nonlinearities in air.

6. Example: ATLAS-3000 at CALA

A concrete realization is the Advanced Titanium:Sapphire Laser (ATLAS-3000) at the Centre for Advanced Laser Applications (CALA) in Garching:

1. Oscillator: Ti:sapphire, \(\sim 80\) MHz, one picked pulse \(\sim 1\) nJ, \(\sim 20\)–30 fs.
2. Stretching: pre-amplifier (booster) + grating stretcher → \(\sim 1\) ns chirped pulse; peak intensity reduced dramatically.
3. Multi-stage amplification: beam expanded stepwise to tens of cm; tens of joules on target while staying below damage and nonlinear limits.
4. Compression: large grating compressor → \(\lesssim 30\) fs (often \(\sim 20\) fs transform-limited); typical on-target energies 10–40 J.
5. Focusing: vacuum transport; off-axis parabolic mirrors. LION (laser–ion acceleration): focus \(\sim 5\) µm FWHM, f/5. LUX (maximum intensity): f/1 pursued. Other beamlines use longer focal lengths (e.g. ETTF wakefield \(\sim 10\) m, HF \(\sim 50\) cm).

Short duration (\(\sim 20\)–30 fs), high energy (tens of joules), and tight focusing combine to peak powers beyond one petawatt — the driver for relativistic laser–plasma interactions in this course.

7. Outlook

We now know how CPA delivers the extreme fields discussed in Lecture 2. Lecture 4 asks what happens when such a pulse meets a real solid target: field ionization, free electrons, and the breakdown of the rigid-mirror picture.

Work through Exercise 3 (Gaussian beam, focal-spot diagnostics) before the tutorial.