Laser-Ion Acceleration

0. Overview

Plasma frequency, critical density, refractive index, group and phase velocity, Debye length. The key message is that a plasma is a dispersive medium and, at high intensity, a transient nonlinear optical element.

1. Electron “swarm” response → dielectric function

Consider a collisionless, cold electron fluid (“electron swarm”) in a homogeneous ion background. An applied laser field displaces electrons by \(x(t)\), creating a restoring force. The basic building blocks are the dipole moment of a single electron and the polarization of the swarm:

Dipole moment: \(\mathbf{p} = -e\,\mathbf{x}\), Polarization: \(\mathbf{P} = n_e \mathbf{p} = -n_e e\,\mathbf{x}\).

For a harmonic drive \(\mathbf{E}(t)=\Re\{\mathbf{E}_0 e^{-i\omega t}\}\), the (collisionless) equation of motion is \(m_e \ddot{\mathbf{x}} = -e\,\mathbf{E}\), so \(\mathbf{x} = \frac{e}{m_e\omega^2}\mathbf{E}\). Hence

\(\mathbf{P} = -n_e e\,\mathbf{x} = -\frac{n_e e^2}{m_e\omega^2}\,\mathbf{E}.\)

Using \(\mathbf{D}=\varepsilon_0\mathbf{E}+\mathbf{P}=\varepsilon_0\varepsilon(\omega)\mathbf{E}\) gives the dielectric function

\(\varepsilon(\omega)=1-\frac{\omega_p^2}{\omega^2}, \omega_p=\sqrt{\frac{n_e e^2}{\varepsilon_0 m_e}}.\)

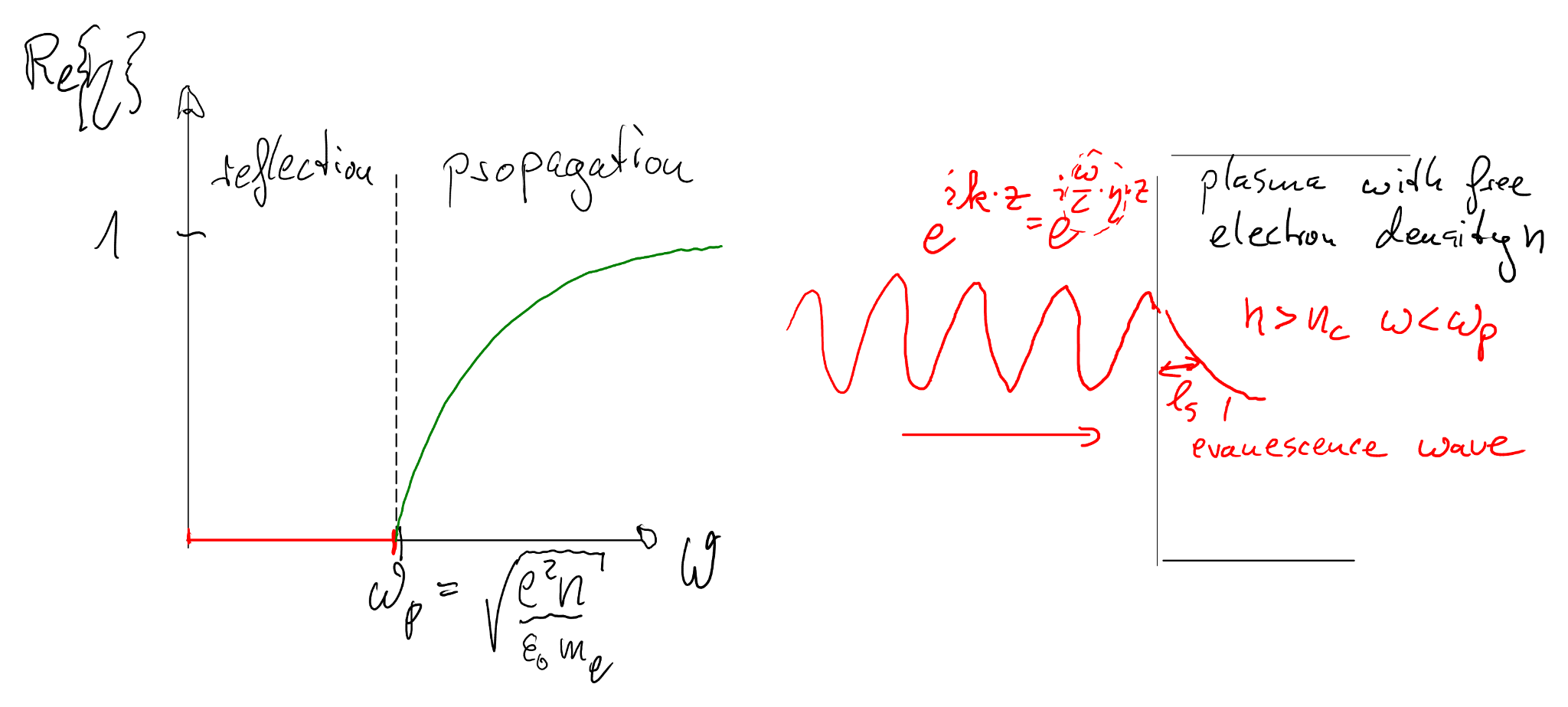
The refractive index is \(n(\omega)=\sqrt{\varepsilon(\omega)}\). Therefore a plasma is dispersive. The critical density for a laser frequency \(\omega\) is defined by \(\omega_p=\omega\):

\(n_c=\frac{\varepsilon_0 m_e \omega^2}{e^2}.\)

2. To propagate or not to propagate

Inserting a plane-wave ansatz \(\mathbf{E}\propto e^{i(kx-\omega t)}\) into the wave equation \(\nabla^2\mathbf{E}-\frac{1}{c^2}\frac{\partial^2\mathbf{E}}{\partial t^2}=\mu_0\frac{\partial^2\mathbf{P}}{\partial t^2}\) yields the cold-plasma dispersion relation:

\(k^2 c^2 = \varepsilon(\omega)\,\omega^2 \quad \Rightarrow \quad \omega^2=\omega_p^2 + c^2 k^2.\)

Phase and group velocity

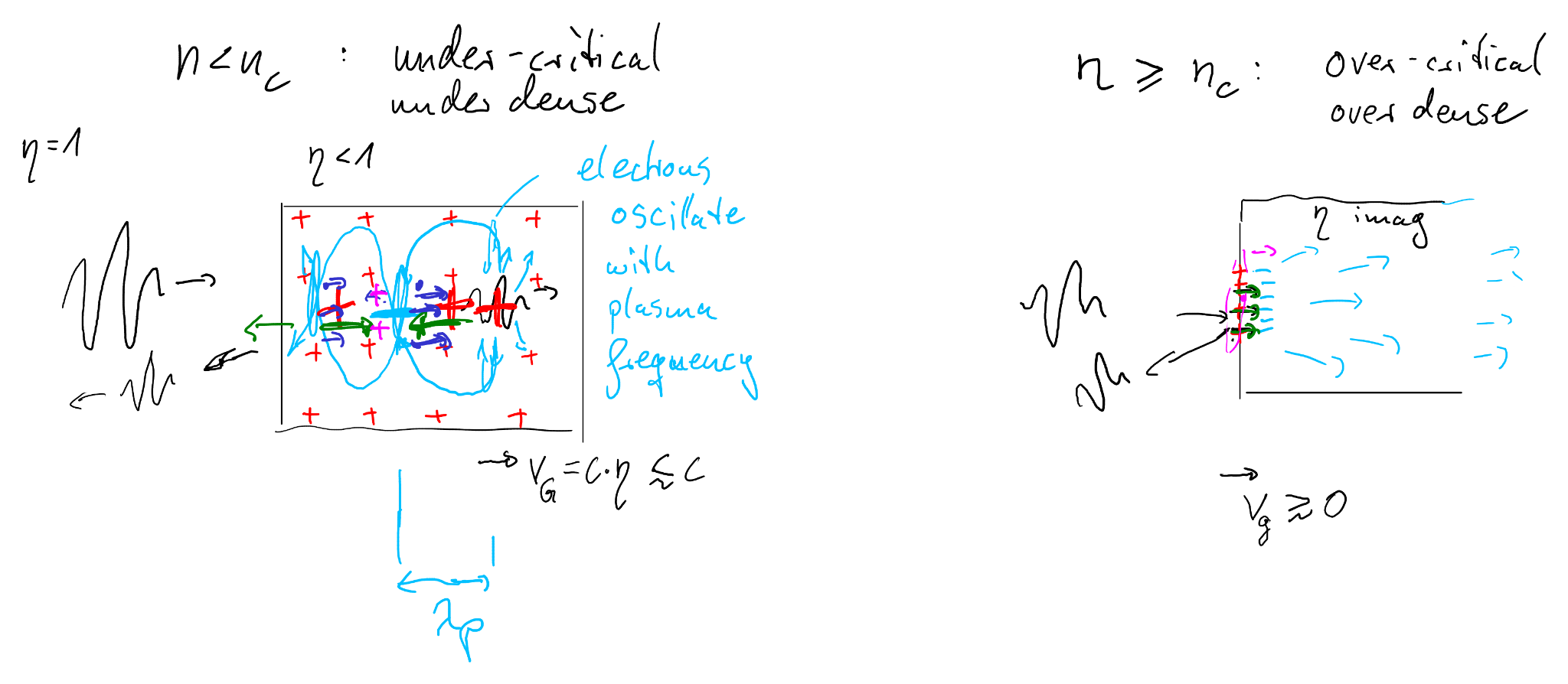
\(v_\varphi=\omega/k=\frac{c}{\sqrt{1-\omega_p^2/\omega^2}}\), \(v_g=\frac{\partial\omega}{\partial k}=c\sqrt{1-\omega_p^2/\omega^2}.\)

So: \(\;v_\varphi v_g = c^2\;\) (phase velocity can exceed \(c\), while energy/information travels with \(v_g<c\)).

This is why a plasma can act as an optic: mirror/reflector near \(n_e\approx n_c\), but also lens/self-focusing medium once \(\varepsilon\) varies transversely.

3. Overdense plasmas and skin depth (evanescence)

For \(n_e>n_c\) the refractive index becomes imaginary. Writing the wave number as \(k=i/\delta\) yields an exponential decay \(E(x)\propto e^{-x/\delta}\) with penetration depth (skin depth) \(\delta\).

\(\delta=\frac{c}{\sqrt{\omega_p^2-\omega^2}} \;\approx\; \frac{c}{\omega_p} \quad (\omega_p\gg \omega).\)

In the strongly overdense limit (\(\omega_p\gg\omega\)), the skin depth is of order \(c/\omega_p\), i.e. on the order of the plasma length scale. Since the plasma wavelength is \(\lambda_p=2\pi c/\omega_p\), one has \(\delta\sim \lambda_p/(2\pi)\) (same order of magnitude).

4. “Slowly evolving” relativistic refractive index

Relativistic motion can be captured (in a simple, slowly-varying model) by replacing \(m_e\to \gamma m_e\), where \(\gamma\) is the cycle-averaged relativistic factor associated with quiver motion. This reduces the effective plasma frequency and modifies the refractive index:

\(\varepsilon(\omega)=1-\frac{\omega_p^2}{\gamma\,\omega^2}, n(\omega)=\sqrt{1-\frac{\omega_p^2}{\gamma\,\omega^2}}.\)

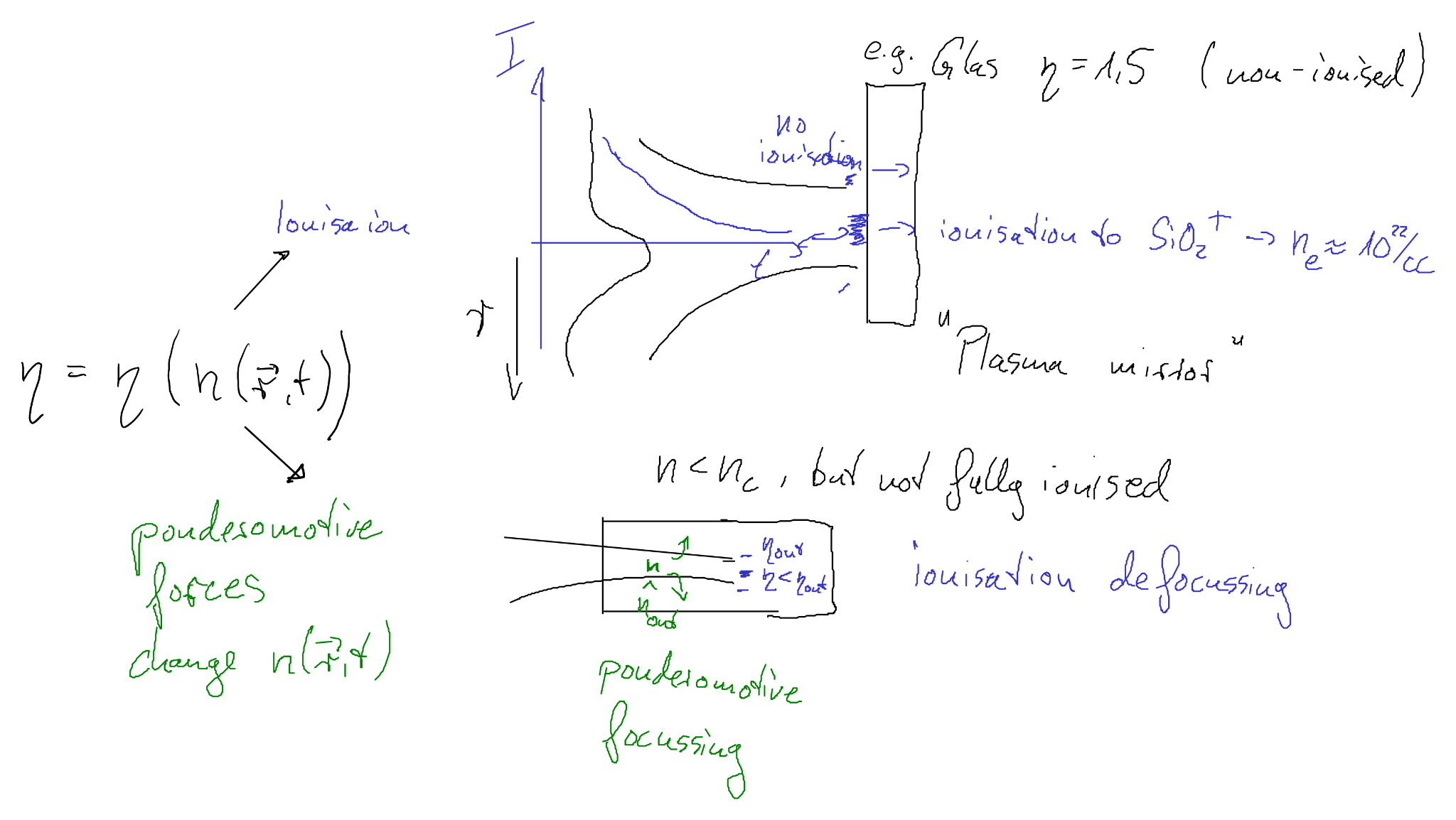
Importantly, both \(n_e\) and \(\gamma\) can vary in space and time due to electron motion in the laser/plasma fields and due to ionization. Hence the plasma is a transient, nonlinear optical element.

Example processes that affect \(n_e\) (and/or \(\gamma\))

• Ionization (non-relativistic): in an underdense medium, ionization increases \(n_e\) and therefore decreases the refractive index → ionization defocusing of a propagating beam.
• If ionization increases \(n_e\) beyond \(n_c\), an initially transparent medium (e.g. a glass plate) can become a plasma mirror.
• Ponderomotive forces: expel electrons from high-intensity regions, reducing \(n_e\) on-axis → refractive index increases on-axis → ponderomotive (self-)focusing can occur.

5. Bottom line